The Quantitative Analysis of Stereoscopic Effect

1. Anaglyphic Image and Stereoscopic Effect

1.1 Anaglyphic Image and Its Relationship between the Focal Plane

Anaglyphic Image is one of the methods for displaying stereoscopic picture. It is based on the principle that red and blue are complementary colors. It is created by using a software tool to combine the left and the right image into a single picture. By looking at an anaglyphic image with an anaglyphic viewer (also called Red and Blue glasses), our left eye will see the red-colored left picture and the right eye will see the blue-colored right picture. Our brain in turn makes them into a stereoscopic picture.

Lenticular printing on the other hand does not require any external visual aid or devices to see stereoscopic images.

The stereoscopic effect of an image is created by the depth of foreground and background in a view. A 2D image on a piece of paper cannot have a stereoscopic effect. From presentation point of view a stereoscopic image is superior to a flat image. For example, Figure 1 is not as spectacular as those anaglyphic pictures in Figure 2 to 6. In a scene, it usually includes three sections; i.e., the foreground, the mid-ground, and the background. (In this article, the foreground means the most frontal portion of a scene and the background is the farthest end of a scene. The mid-ground is anywhere between the foreground and the background). For example, in Figure 1, the smaller wheel on the left is the foreground, the bigger wheel on the right is the mid-ground, and the trees in the back constitute the background.

Please proceed with a pair of RED / BLUE glasses to view the following analyphic images.

 

Stereoscopic image has an important concept: focal plane. It is a 0 thickness plane that intersects vertically with the depth. In an anaglyphic image, the position of the focal plane is in an area where the red and blue images coincide completely. In other words, it is an area where there is no red and blue image. If the focal plane is a window, the objects in front of the focal plane look like they are outside the window. The objects behind the focal plane look like they are inside the window. In Figure 4, the position of the focal plane is on the bigger wheel. Thus, the smaller wheel in the front is outside the window and the trees in the back are inside the window. When you use Photoshop to merge the right and the left image into a anaglyphic image, assuming the right image is static and you are only moving the red left image from left to right, you will notice the window gradually moves from the front to the back in an order seen in Figure 2 to Figure 6.

1.2 The measurement of Stereoscopic Effect

How do we use anaglyphic image to measure stereoscopic effect? We know from the anaglyphic image where stereoscopic effect is shown as double image. Specifically, the stereoscopic effect is the degree of horizontal deviation between red and blue image. Take Figure 3 as an example, the small wooden wheel in the foreground doesn’t have double image thus it is the position of the focal plane. The large wooden wheel in the mid-ground has double image. There is a horizontal deviation in both red and blue image. The double image also occurs in the background which has an even bigger horizontal deviation. The largest horizontal deviation in the background reflects the degree of stereoscopic effect. When the deviation becomes too large, our eyes become irritated. If the horizontal deviation is too small, the stereoscopic effect becomes insufficient. Naturally, the size of horizontal deviation is closely related to the size of the image itself. Therefore, we define the formula for a stereoscopic effect as a ration between an anaglyphic image’s maximum level of deviation and an image’s horizontal distance. It can be expressed as:

c = (δ / r) x 100% -------------------- (1)

Where c is the stereoscopic effect, δ is the maximum level of horizontal deviation, and r is the image’s horizontal distance.

1.3 The Measurement of Maximum Level of Horizontal Deviation

In this formula, the denominator of r which is the image’s horizontal distance, can be easily measured. We only need to get a ruler to measure either on a computer screen or on a picture. On the other hand, to measure the numerator δ (the maximum level of an anaglyphic image’s horizontal deviation) will not be as easy. There are 5 different conditions to consider:

1. When the foreground is on the focal plane. In this condition, we only need to measure the background’s horizontal deviation. (Like Figure 3).
2. When the background is the focal plane. In this condition, we only need to measure the foreground’s horizontal deviation. (Like Figure 5).
3. When the mid-ground is the focal plane. In this condition, we need to measure both the foreground and background’s horizontal deviation and take their reverse deviation by adding them together. (Like Figure 4).
4. When entire image is the focal plane. In this condition, the foreground and the background have the concurrent deviation and the background deviation is greater than that of the foreground. The measurement will be the difference of these two deviations. (Like Figure 2).
5. When entire image is outside the focal plane. In this condition, the foreground and the background have the concurrent deviation and the foreground deviation is greater than that of the background. The measurement will be the difference of these two deviations. (Like Figure 6).

It is not difficult to discover that maximum level of horizontal deviation is based on the horizontal deviations of the foreground and the background and the direction of the horizontal deviation. It is a plus when the focal plane is in the mid-ground otherwise it is a minus.

Thus, the maximum level of horizontal deviation can be concluded as the horizontal deviation difference between the foreground and the background. The table below shows the measurements of Figure 2 to Figure 6 and their values of stereoscopic effect.

	Foreground Deviation (mm)	Background Deviation (mm)	Maximum deviation δ (mm)
Figure 2	2	10	8
Figure 3	0	8	8
Figure 4	-2	6	8
Figure 5	-8	0	8
Figure 6	-10	-2	8
r = 237mm c = (δ / r) x 100% = 8 / 237 = 3.4%

1.4 The Statistical Analysis Result of Stereoscopic Effect

The author has collected more than 40 high quality anaglyphic images from the Internet. Based on the above mentioned methods, the author measured these images on computer screen and calculated the values of their stereoscopic effect. The results of statistical analysis, almost all the images’ stereoscopic effect values are between 1% and 4% with the average value at 2.5%.

c = 2.5% ± 1.5%

It was found during the process of statistical analysis that for those images with a very large depth (e.g, long streets), their stereoscopic effect values are greater. Likewise, the images with a shallower depth (e.g. portraits,) their stereoscopic effect values are smaller. This coincides with the stereoscopic effect formula inferred below.

Due to the limited statistical sampling, these values might not be exactly accurate. However, they possess certain reference value. Accuracy of these values relies on higher samples numbers and the image.

2. The Inferential Reasoning Behind the Stereoscopic Effect’s Formula

2.1 The Determination of Image’s Horizontal Distance

In the Stereoscopic Effect formulas, we need to determine two variables, namely the horizontal distance r and the horizontal deviation δ. First, let’s look at how to calculate image’s horizontal distance r.

No matter how complicated a camera’s lens is, in general you can view it as a convex lens (As shown in Figure 7).

In Figure 7, α is the viewing angle of a lens, the focal length is f, the width of the photosensitive part is d (please note it is not the length of the diagonal line). The width of the object is r and the distance from the lens to the object is u. When the object’s distance is long enough from the lens, you will find r / d = u / f. Hence

r = (d / f) x u -------------------- (2)

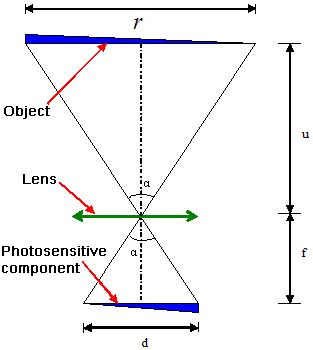
This is to say, when the width of camera's photosensitive d and lens' focal distance f have been determined, the width of the scenery r and the object’s distance u are in direct ratio.

2.2 The Inferential Reasoning

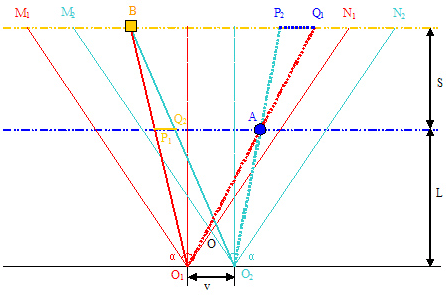
In Figure 8, O₁ and O₂ are the locations of the left and the right lens. The lens axis (lens distance) is v. The lens’s viewing angle is α. M₁O₁N₁ is the viewing area of the left lens. M₂O₂N₂ is the viewing area of the right lens. M₂ON₁ is the cross section of these two lenses.

L is the distance between the lens and the foreground scenery. The distance from the lens to the background is L + S. It means S is the depth of view. A is any point in the foreground. B is any point in the background.

2.2.1 When Foreground is the Focal Plane

In this case, the horizontal deviation distance of the B point in the background is δ₁ = P₁Q₂. Please note, the triangle P₁BQ₂ and triangle O₁BO₂ are similar. Thus Δ P₁BQ₂ ≈ O₁BO₂, thus δ₁ / v = S / L + S, δ₁ = vS / L + S. From formula (2) we know, r₁ = (d / f) x L. We will have the stereoscopic effect formula when we plug in Δ₁ and r₁

c =(vS f) / [dL(L + S)] -------------------- (3)

2.2.2 When Background is the Focal Plane

When background is the focal plane, the horizontal deviation of A point in the foreground is δ₂ = P₂Q₁. As shown in Figure 8. Please note, Δ P₂AQ₁ ~ O₁AO₂, thus δ₂ / v = S / L + S, δ₂ = vS / L + S. From formula (2) we know, r₂ = d / f x (L + S). When we plug δ₂ and r₂ in formula (1), we get the same formula (3). Is this coincidental? Please read on.

2.2.3 When Mid-ground is the Focal Plane

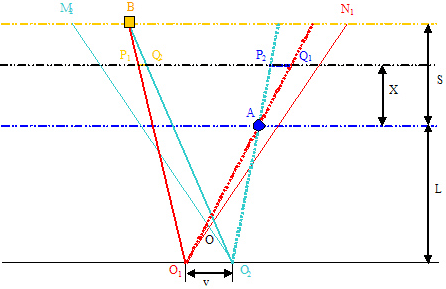
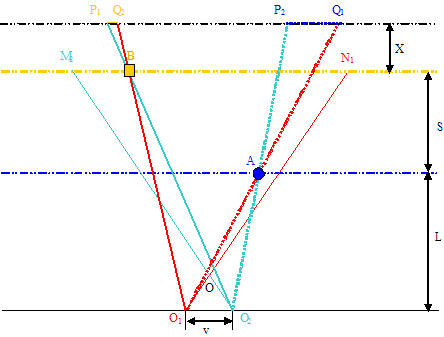
In Figure 9, there is a focal plane line between the foreground and the background. Let’s denote X as the distance from the line to the foreground. In this case, the horizontal deviation for the A point in the foreground is P₂Q₁. The B point in the background is P₁Q₂.

The horizontal deviation of A point, Δ P₂AQ₁ ~ Δ O₁AO₂, hence P₂Q₁ / v = X / L, P₂Q₁ = vX / L.

The horizontal deviation of B point, Δ P₁BQ₂ ~ Δ O₁BO₂, hence P₁Q₂ / v = S - X / L + S, P₁Q₂ = v(S - X ) / L + S.

The total horizontal deviation, δ₃ = P₁Q₂ + P2Q1 = vX / L + v(S –X) / L + S = vS(L + X) / L(L + S)

From formula (2), r₃ = d / f x (L + X). Plug δ₃ and r₃ into formula (1), we also get the stereoscopic effect formula (3). This formula has no relationship with X.

2.2.4 When Entire Image is Outside the Focal Plane

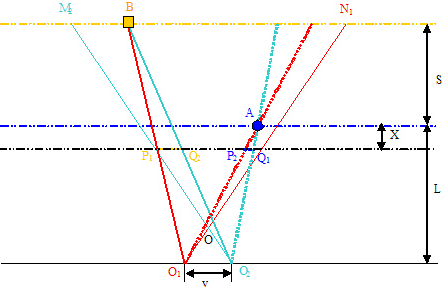
In this case, all the objects are in front of the focal plane as shown in Figure 10. Assume the distance from the focal plane to the background is X.

The horizontal deviation of A point, ΔP₂AQ₁ ~ ΔO₁AO₂, hence P₂Q₁ / v = S + X / L, P₂Q₁ = v(S + X) / L.

The horizontal deviation of B point, ΔP₁BQ₂ ~ ΔO₁BO₂, hence P₁Q₂ / v =X / L + S, P₁Q₂ = vX / L + S

The total horizontal deviation, δ₅ = P₂Q₁ - P₁Q₂ = v(S +X ) / L + S – vX / L + S = vS(L + S + X) / L(L + S)

From formula (2), r₅ = d / f x (L + S + X). Plug δ₅ and r₅ into formula (1), we also get the stereoscopic effect formula (3).

2.2.5 When Entire Image is Outside the Focal Plane

One item that needs attention is that the r, the image’s horizontal distance (length) is actually a constant. It is due to lens’ perspective, we see the distance difference in r₁ to r₅.

The results of the 5 conditions all lead to the stereoscopic effect formula (3). In other words, an image’s stereoscopic effect is not related to relative position of the focal plane. It was decided when the picture was taken. This is the inherent characteristic of a stereoscopic image.

2.3. Formula’s Further Development

The formation of an image through a lens follows the rule of 1 / u + 1 / i = 1 / f where i is the image distance. When u the object distance, the distance between lens and the object is sufficiently large, i approximately equals to the focal distance f. For example, when we use a 50mm lens to take a picture of an object 5 meters away the image distance is 50.5mm. The relative error between the image distance and the focal distance is (50.5 – 50) / 50 = 1%. The longer the object distance is the smaller the relative error. In this case, image’s horizontal distance calculation formula (2) can be established. In other words, stereoscopic effect formula (3) is only suitable for mid range photography. What about short range photography?

It is actually pretty simple. If we treat the object we are taking in its entirety, the distance between the lens and foreground becomes the object distance (L = u), from the image formation formula we get i = Lf / L –f. In formula (3), we replace focal distance f with the image distance i, we get:

c = (vSf) / d(L –f) (L + S) -------------------- (4)

There is not much difference between formula (4) and formula (3). When L is large enough (greater than f), L - f ≈ L, formula (4) degrades to formula (3).

In micro photography, the object is very close to the lens, usually measured in few decimeters. But the depth of field is even shorter, only in few millimeters. In this situation, L is greater than S, L + S ≈ L, Formula (4) degrades to:

c = (vSf) / [dL (L - f)] -------------------- (5)

To summarize it, amongst the three stereoscopic effect formulas, formula (3) is suitable for mid range photography. Formula (4) is suitable for close range photography and formula (5) is suitable for micro photography. And formula (4) has the comprehensive nature. The other two formulas may derive from it through simplification.

3 The Explanations and Analysis of the Formulas for Stereoscopic Effect

3. 1. The Formulas’ Inferential Basis

The above stereoscopic effect formula is derived from anaglyph. In fact, its theory is similar to that of parallel graph and interlacing graph. The only difference is that anaglyph is more straightforward and easier to be surveyed and measured.

3.2 Suitable Lens for These Formulas

There was a hidden hypothesis during the process of inferring these stereoscopic effect formulas. It was assumed that the viewing field of a camera’s lens is flat. It is only reasonable in such a condition to treat focal plane as a flat plane. The actual viewing field should be spherical but the lens adjusts this spherical viewing field into a flat plane viewing field. The bigger viewing angle of a lens, the more obvious spherical plane there is. It is harder to make adjustment when a wide-angle lens is used due to barrel-like distortion. Thus these stereoscopic effect formulas are only suitable for mid and long range lens and a type of wide-angle lens that can control distortion. It is completely unsuitable for fish-eye lens.

3.3 Explanations on Formula’s Parameters

All the parameters in the stereoscopic effect formulas are unit of length. The resultant value of stereoscopic effect is very small. The values in d, l and v are measured in mini-meter. In mid-range photography, the L and S are measured in meter which is two number magnitudes larger. In micro-range photography, The L, d, f and v are measured at the same level while the S is two number magnitudes smaller.

To see the impact of these parameters to the stereoscopic effect, we can take a look at the c, which is the value of stereoscopic effect. It will increase when the v, f, and S increase. On the other hand, it will decrease when the L and d decrease.

Each parameter has its own order. First, the camera determines the value of the d, the lens determines the value of the f, then after the scene has been selected, it determines the value of the L and S. Finally, after picture is taken, it determines the value of the v. Therefore, when taking a stereoscopic picture, the lens distance v is the most nimble and the most controllable. It is also a parameter that has the biggest impact.

3. 4 The Focal Distance f and Its Linkage to Other Parameters

In the stereoscopic effect formulas, a parameter's change will cause other parameter to change. We will analyze the impact on other parameters when the value of focal distance, the f is changed. For this analysis, we will use three scenarios in mid-range photography.

1. The location of the camera does not change. It means the L doesn’t change. If the focal distance f is doubled, the area of photography will reduce four times as much. In other words, the distance of the object will reduce 2 times. The depth of field S stays the same since what we compare is the common portion after the shrinking scope of the area. The parameter d doesn’t change either. If we want to maintain the same stereoscopic effect in formula (3), one way to do it, is to reduce focal distance by 100%. In other words, in this situation, the lens distance v and the focal distance f are inversed.
   
   
2. The scenery stays the same but the location of the camera is changed. If focal distance f increases by 100%, the photographer can only retreat by 100% of the distance. It means to increase L by 100%. Because the size of the scene doesn’t change, thus the depth of field S doesn’t change either. The parameter d doesn’t change either. If we want to maintain the same stereoscopic effect, one way to do it, is to increase the lens distance v which should be less than 100%. According to formula (3), if f is changed to n times, then v change will be nL + S / L + S < n times. That means, in this condition lens distance and focal distance are changed concurrently. But v’s change should be less than that of f.
   
   
3. Only f and d are changed, not others. When focal distance f increases to N times is equal to d decreases N times.
   
   When the value of d is changed, it means the camera is changed. Take a digital SLR camera and a regular digital camera for example, the photosensitivity in former camera is greater than that of the latter. If we only consider the photosensitivity’s impact to the stereoscopic effect based on its Inverse proportion with d, the latter camera is more suitable for stereoscopic photography. From the angle of depth of field, the latter camera has a longer depth of field which is required in stereoscopic images.

3. 5 The Photography’s Exceptional Case

When using a 135 camera (d = 36mm) with a 50 mm standard lens for mid-range photography. The formula (3) can be simplified into c = 1.389 x v S / L (L + S).

Then based on using the 1/50 lens distance experience, v / L = 1/50, we get c = 1.389 x 1 / 50 x S /(L + S) = S / (L + S) x 2.78% < 2.78%. This is to say that under such shooting condition, stereoscopic effect value shouldn’t exceed 2.78%.